Problem Statement

Consider the following problem:

We wish to visit every node of a $k$-simplex (i.e. k-dimensional generalization of Pascal’s triangle) exactly once, in arbitrary order defined by some value function $v(n)$, with the condition that $v(m) < v(n)$ if $n$ is a child of $m$.

For the purposes of this problem, we consider each node of the simplex to be given as its coordinates

$$n = (x_0, x_1, …, x_{k-1}) ; x_j \in \mathbb N $$

A node is said to have children

$$\{ (x_0, x_1, …, x_i + 1, …, x_{k-1}) | i \in [0,k) \}$$

Note that any node will appear as the child of up to $k$ parent nodes.

This problem appears in, e.g., enumerating the $B$-smooth integers in ascending order: here the simplex has $k = \pi(B)$ dimensions, with coordinate of each dimension $j$ the power of $p_j$ in the factorization of the numbers, and $v(n)$ is accordingly $\prod_{i=1}^k p_i^{x_i}$

Existing Python Solutions

The “standard methodology” for doing this in Python, as I could find it, is recursive generator magic in the style of this algorithm.

This certainly works and satisfies some definition of elegance. However, it doesn’t quite satisfy my definition of elegance: I find “hidden, recursive generators” to be highly opaque and unpleasant to think about.

To that end, I wanted to come up with a simple, explicit heap-based solution.

The Naive Attempt

When writing a heap-based algorithm, the goal algorithm is “unrolled recursion”, where every node puts its valid children on heap keyed by $v$, and we run until the heap is exhausted, or some other condition is satisfied:

# we wish it was as simple as this!
heap = [(v0, [0] * k)]
while heap:
    v, parent = heappop(heap)
    yield v, parent
    for i in range(k):
        child = parent.copy(); child[i] += 1
        v_i = calculate_v(child)
        heappush(heap, (v_i, child))

The problem with this is duplicates! Every node will be visited a very large number of times (indeed, this number is given by the associated multinomial coefficient!), instead of once.

The Intuition

This problem would be trivial if we could traverse the simplex like a grid in a fixed order. There, we have a simple rule for incrementing the position without repeats – the same as for a multidimentional array: the outer loop reaches all children, the next inner loop reaches children in a subarray of dimension $k - 1$, the next one of $k - 2$, and so on, until the innermost loop reaches only children in one dimension.

To build our intuitions, we can visualize standard array traversal as transforming our array into a tree:

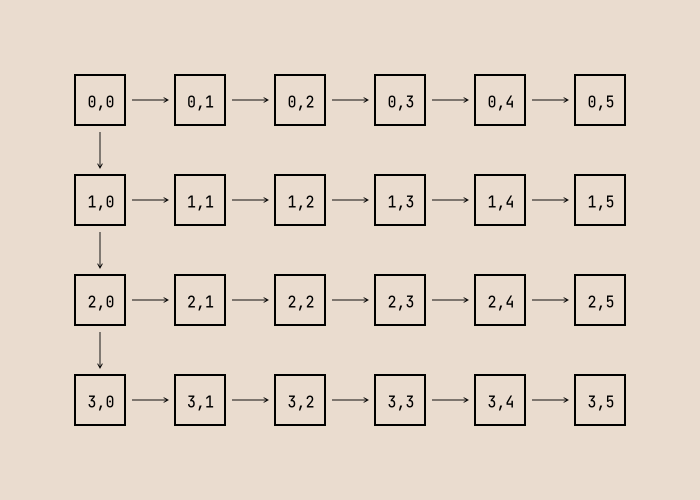
We can see that nodes on the left each have two children, all other nodes have one child. However, we must satisfy the property that:

$$ v(m) < v(n) \implies m \text{ is expanded before } n $$

Which means we cannot do the obvious thing and walk “layer by layer” in the outer loop, and then within a layer in the inner loop (and so on recursively for all dimensions), since the node with the lowest $v$ in a given layer may appear anywhere, including at the “leaves” of a layer-ordered traversal.

However, we can still apply the same traveral strategy if we traverse diagonally:

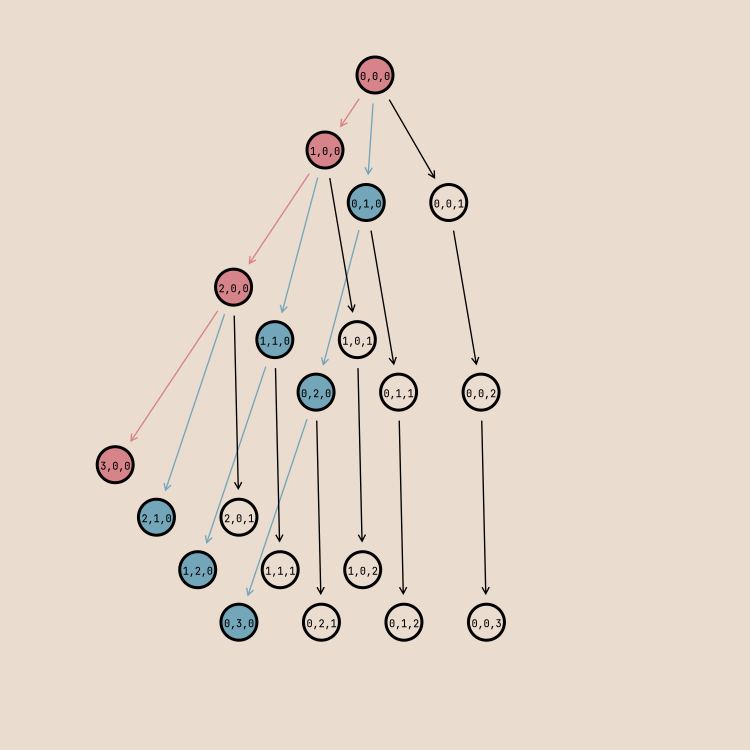
One can quickly convince oneself that in the above traversal scheme, a node’s position in the output order is never missed. That is because, critically, every node’s parent in the traversal tree is also a parent in the simplex. Assume, that node $n$ in layer $l$ is missed. Then its traversal-parent $p$ (which is also a simlex-parent) in layer $l - 1$ must have been missed as well; otherwise, the parent would have come before $n$ on the heap since by assumption $v(p) < v(n)$, and in being expanded would have put $n$ on the heap. This is an absurdity by infinite descent on $l$; therefore no node is missed.

How can we express the above traversal in code? The nodes have been suggestively colored by the number of children they have, and the arrows indicate the color of the child. What we want is a way to get this color – e.g. if it’s a corner, side, or linear node – even if seeing it in an arbitrary order. If we look hard at the coordinates of the respective node types, we can infer the following rule:

Define a node’s weakness:

$$ \begin{align} w(0) &= 0 \\ w(n) &= k - \#(\text{coordinate trailing zeros in } n) - 1 \end{align} $$

Then we expand according to the following rule:

A node $n$ of weakness $w$ will expand into $k - w$ children given by $\{(x_1, …, x_j + 1, …) | w \le j < k \}$

For example:

1. $(x_0, 0, 0)$ with $w=0$, and so will expand into $(x_0 + 1, 0, 0), (x_0, 1, 0), (x_0, 0, 1)$.
2. $(x_0, x_1, 0)$ with $w=1$, will have only two children, $(x_1, x_1 + 1, 0)$ and $(x_0, x_1, 1)$.
3. $(x_0, x_1, x_2)$ with $w=2$ will have a single child, $(x_0, x_1, x_2 + 1)$

The Algorithm

Let’s modify our naive algorithm above:

heap = [(v0, [0] * k, w)]   # <- we cache the weakness value
while heap:
    v, parent, w = heappop(heap)
    yield v, parent
    # our weakness restricts us to the subspace of dimension k - w of trailing
    # coordinate values.
    for i in range(w, k):
        child = parent.copy(); child[i] += 1
        v_i = calculate_v(child)
        # the child node's weakness is just the incremented coordinate!
        heappush(heap, (v_i, child, i))

As we can see, it’s a very remarkably small change to the naive “ideal” algorithm, and will visit each node exactly once.

Generalizing

The traversal above is very similar to breadth first search. Indeed, we could also have kept an open set of previously seen nodes to avoid duplicates while doing the naive traversal. However, that approach has a runtime or memory penalty, as we would need to look up every double-expanded child in some table. With the monotonicity property of $v$, that is not necessary in this case.

However, this prompts the question: in what cases can search with use of an open set be replaced with a similar weakness function? The correctness proof above relies on only the following property. Given the traversal tree $T$ induced by $w$:

1. $\forall u: \{ n | v(n) \le u\}$ is reachable from the root in $T$.

Any weakness function $w$ whose induced traversal tree satisfies the above relationship will guarantee no node is missed.

Keep an eye out for graph traversals where an open set lookup can be replaced by a weakness function!